[HAM] 직교위상 신호(Quadrature Signals)는 복잡하지 않다. 복합적 일 뿐, (3/5)
A Quadrature Signals Tutorial: Complex, But Not Complicated
by Richard Lyons
[ 원본출처: https://dspguru.com/dsp/tutorials/quadrature-signals/ ]
---------------------------------
주) 아래 번역 중 [] 안의 내용은 제가 부연설명 삼아 추가한 것입니다. 틀릴 수 있으니 미리 양해를 구합니다. 오류나 미진한 부분이 있다면 기탄없는 지적 바랍니다. -역자-
---------------------------------
<이전>
Representing Quadrature Signals In the Frequency Domain
직교위상 신호(페이저)를 주파수 영역에서 표현하기
Now that we know something about the time-domain nature of quadrature signals, we're ready to look at their frequency-domain descriptions. This material is critical because we’ll illustrate the full three-dimensional aspects of the frequency domain.
이제 직교위상 신호가 어떻게 표현되고 어떤 특성을 가지는지 시간영역(time-domain)에서 살펴 보면서 어지간히 감은 잡았으리라 생각된다. 이번에는 좀 난해할 텐데 주파수 영역(frequency-domain)의 특징을 3차원으로 살펴볼 참이기 때문이다.
[실수와 허수 평면에 주파수 축을 더해서 살펴보려 한다. 앞서 시간의 축이 가미된 그림으로 그렸을 때 나선형의 모습으로 나왔던 페이저는 사실 2차원 상에서도 충분히 설명 할 수 있었다.]
[삼각함수의 파(코사인 파 또는 사인파)를 주파수 축의 임펄스로 표현한다. 이 임펄스는 시간에 따라 회전하는 페이저가 아니다. 시간에 독립적인 주파수 성분을 나타낸다. 또한 식 (10)과 (11)에서 봤듯이 복소수로 표현된 임펄스는 주파수는 양수 및 음의 값을 가질 수 있다. 또한 진폭도 양 또는 음의 값을 가진다. 복소수로 표현되는 임펄스는 동일한 진폭, 동일한 주파수를 가진 삼각함수의 파에 대해서도 실수부와 허수부에 의해 상대적 위상으로 구분 될 수 있다.]
That way none of the phase relationships of our quadrature signals will be hidden from view. Figure 8 tells us the rules for representing complex exponentials in the frequency domain.
그래도 이런식으로 다룸으로써 직교위상 신호의 위상에 대한 연관성을 확연히 드러난다. 그림 8은 주파수 영역에서 페이저를 표현한 복소지수함수의 각 부분의 의미를 설명하였다.
Figure 8. Interpretation of complex exponentials.
그림 8. 복소지수식에서 각 부분의 의미
We'll represent a single complex exponential as a narrowband impulse located at the frequency specified in the exponent. In addition, we'll show the phase relationships between the spectra of those complex exponentials along the real and imaginary axes of our complex frequency domain representation.
단일 복소수 지수식(single complex exponential)을 지수부에 특정한 주파수에 위치한 좁은 임펄스로 표현하는 법에 대해 알아보도록 한다. 덧붙여 허수축 값과 실수축의 값을 달리하는 다수의 복소지수식 사이의 상대적 위상차도 주파수 영역에서 표현해 볼 것이다.
[우리말로 옮기기 굉장히 어렵다. 이것을 영어로 써놓으면 원어민들은 과연 이해하는지 의구심이 든다. 무슨 뜻인지 직관적으로 받아들여 보자.]
With all that said, take a look at Figure 9.
이상에서 말한 것들을 감안하고 그림 9를 보자.
Figure 9. Complex frequency domain representation of a cosine wave and sine wave.
그림 9. 복소수 페이저를 주파수 영역에서 코사인과 사인파로 표현
See how a real cosine wave and a real sine wave are depicted in our complex frequency domain representation on the right side of Figure 9. Those bold arrows on the right of Figure 9 are not rotating phasors, but instead are frequency-domain impulse symbols indicating a single spectral line for a single complex exponential e^(j2πf_0t). The directions in which the spectral impulses are pointing merely indicate the relative phases of the spectral components. The amplitude of those spectral impulses are 1/2.
실 코사인파와 실 사인파를 복소 주파수 영역에 표현하면 그림 9의 오른편의 그림과 같다. 굵은 화살표는 회전하는 페이저가 를 나타낸 것이 아니다. 이 화살표는 [주파수 영역에서 주파수 성분을 나타내는] 임펄스 기호(impulse symbol, 폭은 의미를 갖지 않고 성분의 유무만을 표현하는 삐죽 솟은 표시(기호)])로 복소지수(complex exponential=phasor) e^(j2πf_0t)의 스펙트럼 선이다 [e^(j2πf_0t)는 시간 영역에서는 회전하는 페이저였다.] 스펙트럼 선의 방향은 스펙트럼 성분의 상대적인 위상(relative phase)을 가리킨다. 이 스펙트럼 선의 높이는 1/2 이다.
[상대적인 위상(relative phase): 위상(phase)에 대한 이해가 필요한 시점이다. 위상은 단적으로 말하면 각도다. 이 각도가 시간에 따라 변하면서 주기를 갖는 정현파(sinusoid wave)를 만들어 낸다. 주기파형의 특성을 표현하는 주파수는 시간 영역에서 페이저의 초당 회전한 바퀴수다. 이 주기함수를 회전하는 원으로 표시하거나 파동으로 그려낼 때도 있다. 회전이 시작되는 각도에 따라 기준 위치가 달라질 수 있지만 근본적으로 주기함수의 성질이 달라지는 것은 아니다. 그런데 동일한 주기함수라도 시작하는 기준 각도가 달라지면 주기함수를 구분 할 수 있다. 이런 특성을 이용한 변조 방식이 위상변조다. 주파수 대역과 진폭은 변하지 않고도 위상을 바꿈으로써 정보를 실을 수 있다(phase-shift keying).]
OK ... why are we bothering with this 3-D frequency-domain representation? Because it's the tool we'll use to understand the generation (modulation) and detection (demodulation) of quadrature signals in digital (and some analog) communications systems, and those are two of the goals of this tutorial. However, before we consider those processes let's validate this frequency-domain representation with a little example.
다 좋다. 그런데 뭐하러 3차원 주파수 영역을 도입해서 골머리를 앓고 있는가? 왜냐면 디지털 통신(아날로그 통신도 포함하여)에서 직교위상 신호처리를 이해할 때 신호를 뽑아내고(demodulation, 복조[고주파 전파(반송파)를 성분을 거르고 베이스 밴드 신호를 뽑아냄]) 검파(detection, [뽑아낸 베이스 밴드 신호에서 정보를 ])하는 도구로 유용하기 때문이다. 이 교재에서 3차원 주파수영역에서 신호를 들여다 보는 목적이기도 하다. 하지만 더 들어가기 전에 예를 한가지 들어 보겠다. [복조(de-modulation)와 검파(detection)를 구분하자.]
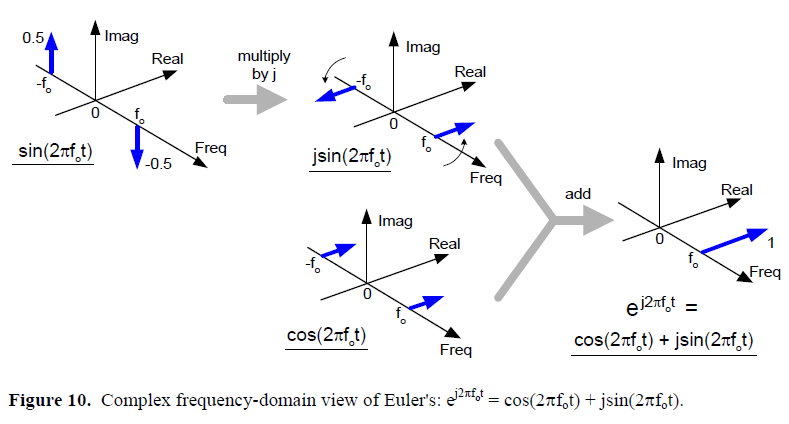
Figure 10 is a straightforward example of how we use the complex frequency domain. There we begin with a real sine wave, apply the j operator to it, and then add the result to a real cosine wave of the same frequency. The final result is the single complex exponential e^(j2πf_0t) illustrating graphically Euler's identity that we stated mathematically in Eq. (7).
그림 10은 복소주파수영역[주파수 성분을 복소수로 기술 하는 것]을 어떻게 활용하는지 직관적으로 보여주는 예다. 먼저 실제 사인파를 보자 [자연현상으로써 존재하는 삼각함수 파(사인파, 코사인파)는 복소수 평면으로 표현하면 양의 주파수와 음의 주파수를 가지고 있다. 수학적으로 식 (10)과 (11)에서 증명한 바 있다.] 이 사인파에 j-연산자를 적용[복소수 평면에서 표현된 한 점에 j를 곱하면 반시계 방향으로 π/2 만큼 회전한다.]하고 이를 동일한 주파수를 가진 실제 코사인 파와 더한다. 단일 복소 지수(single complex exponential) e^(j2πf_0t)를 그림으로 식 (7)의 오일러 등가식에 의거하여 그림으로 나타낸 것이다.
[single complex exponential: 단일(single)은 주파수가 f_0로 한개의 주파수 성분만을 가지고 있는 삼각함수 파의 주파수 성분(임펄스)을 복소수 평면에서 표현 했다.]
[오일러 등가식은 복소수 공간에서 한 점(위치)를 극좌표 형식으로 나타내는 수학적인 표현법이다. 시간영역의 페이져든 주파수 영역의 임펄스든 오일러 등가공식을 적용할 수 있다.]
Figure 10. Complex frequency-domain view of Euler's: e^(j2πfot) = cos(2πf_0t) + jsin(2πf_0t).
그림 10. 복소 주파수 영역에서 본 오일러 공식:
On the frequency axis, the notion of negative frequency is seen as those spectral impulses located at -2πf_0 radians/sec on the frequency axis. This figure shows the big payoff: When we use complex notation, generic complex exponentials like e^(j2πft) and e^(-j2πft) are the fundamental constituents of the real sinusoids sin(2πft) or cos(2πft). That's because both sin(2πft) and cos(2πft) are made up of e^(j2πft) and e^(-j2πft) components.
주파수 축에서 -2πf_0 라디안/초의 지점에 음의 주파수를 갖는 스펙트럼 임펄스를 볼 수 있다. [주파수가 음수가 될 수 있을까?] 이 그림이 주는 큰 혜택이라면, 복소수 형식의 표현을 사용할 때 e^(j2πft) 나 e^(-j2πft) 같은 복소지수의 표현은 실제 삼각함수 파 sin(2πft) 또는 cos(2πft)의 기초 요건이기 때문이다. 왜냐하면 sin(2πft) 또는 cos(2πft)와 같은 실제 삼각함수 파는 e^(j2πft) 와 e^(-j2πft)의 성분을 모두 가지고 있기 때문이다. [실제 삼각함수 파를 복소수 체계의 수학으로 묘사하면 양수의 주파수 성분과 음수의 주파수 성분이 모두 있어야 한다.]
If you were to take the discrete Fourier transform (DFT) of discrete time-domain samples of a sin(2πf_0t) sine wave, a cos(2πf_0t) cosine wave, or a e^(j2πf_0t) complex sinusoid and plot the complex results, you'd obtain exactly those narrowband impulses in Figure 10.
If you understand the notation and operations in Figure 10, pat yourself on the back because you know a great deal about the nature and mathematics of quadrature signals.
그림 10에서 보인 연산과정을 이해 했다면 스스로 등을 두드려 주기 바란다. 직교위상 신호처리의 본질을 상당부분 이해한 것이나 다름 없다.
-------------------------------
<계속>





댓글 없음:
댓글 쓰기