[HAM] 아마추어 무선의 불안한 미래 그리고 디지털 필터
나의 최애 취미는 공부하기다. 이 취미를 꼽는 이유는 즐기는데 소요되는 비용이 매우 저렴하다는 것도 한몫한다. 연필과 종이 그리고 약간의 인터넷 비용이 들 뿐이다. 사실 가진것 없이 일찌감치 은퇴를 했으니 비용이 드는 취미를 가질 처지도 아니다. 그 다음으로 꼽으라면 아마추어 무선. 어느 취미가 그렇지 않으랴 만 장비병에 걸리면 이겨낼 장사없는 취미이긴 하다. 다행히 무서운 장비병이 비껴 갔으니 참으로 다행이다.
앞서 IEEE Spectrum 기사로 실렸던 '아마추어 무선의 불안한 미래'라는 글[바로가기]을 옮겼었다. 사실 아마추어 무선의 미래가 '불안'한 것이 아니라 어디로 튈지 모른다는 느낌으로 읽었다. 한 세기 전의 무선통신 개척자들은 모두 아마추어 통신가들 이었다. 사실 그들 대부분은 통신 전문가라기보다 모험가 였기에 전성기도 짧게 끝나고 이내 제도에 묶여 버렸었다. 이론기반이 빈약하고 무모했던 아마추어들은 결국 전문가들의 통제 영역에 놓이게 됐었다. 그후 한세기가 지난 지금 첨단 정보기술이 아마추어 무선이라는 취미에 응용되어 장비면에서 가히 혁명적이라 할 정도다. 이 혁명이 평균 연령이 60대인 아마추어 무선 취미가들을 위협하는 것은 아닐까? 50년 묵은 진공관식 무전기를 애지중지 하면서 전신 통신술을 구사할 줄 안다며 정통 아마추어 무선사 입네 은근히 재고있는 60대의 나는 이 위협을 떨쳐내고자 오늘도 연필과 종이를 들고 문제를 풀고 있다.
'정통' 아마추어 무선사를 위협하는 신기술에 디지털 필터라는 것이 있다. 여기서 '필터'는 특정 주파수의 신호성분을 차단시키거나 통과 시켜준다는 그 필터 맞다. 이미 백여년전부터 모든 현상은 주기함수와 급수의 합으로 표현될 수 있다는 수학이 확립되어 있었다. 다만 급수합 계산에 너무나 많은 곱셈과 덧셈이 필요하기에 현상 해석용으로 활용 됐다. 반도체 기술이 발달하고 고속 계산이 가능한 디지털 계산기가 상용화 하자 골치아픈 컨덴서와 코일의 조합으로 안정된 필터를 만들고자 했던 눈물겨운 노력들은 이제 무전기에서 사라졌다. 급수합의 '마법'이 디지털화 되어 실시간 활용에 쓰이고 있다. 그중 한 부분이 디지털 필터다.
'급수합의 마법' 이란 디지털화 한 일련의 입력 신호에 특별히 잘 구해진 계수값을 곱하여 이를 더하면 아주 신통한 결과를 얻게 된다. 급수합을 수학으로 표현하면 다음과 같다.

[출처] https://en.wikipedia.org/wiki/Finite_impulse_response
위의 수식은 아주 단순하여 누구나 한눈에 알아볼 수 있다. 다만 첨자에 유의하자. x[n-i] 는 디지털 화한 입력 신호다. b[i] 는 특별한 목적으로 구한 계수다. x[n-i]와 b[i]를 곱한 후 모두 더하여 y[n]을 구한다. 계수에 따라 스펙트럼 분석기가 되기도 하고 필터가 되기도 한다. 변조기가 되거나 복조기가 된다. 이 특별한 계수를 구하는 방법 역시 백년 전부터 잘 알려진 수학으로 '신호처리'라는 과목으로 배운다. 현대 과학기술자들에게 '급수합의 마법'은 마치 구구단 같은 것이어서 이를 당연히 여긴다. 이 계수를 구하는 방법이 아주 까다롭기에 실제로 이를 손수 구하는 경우는 없다. 이를 대신 해주는 다양한 디지털 신호처리 도구(소프트웨어)들이 있다. 디지털 필터용 계수를 구해주는 온-라인 도구는 T-Filter, http://t-filter.engineerjs.com/ 가 있다. 무료로 쓸 수 있다.
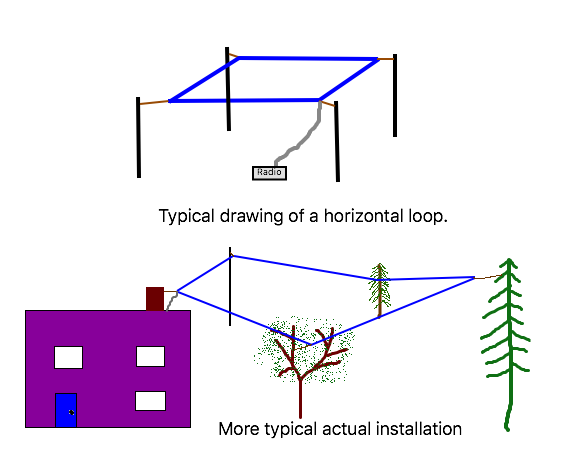
아듀이노 보드를 SSB 수신기의 음성출력을 대상으로 전신신호용 디지털 필터로 활용할 목적으로 다음과 같이 설계했다.

설계 조건이 매우 느슨하게 주어졌다. 8비트 범용 마이크로 컨트롤러용를 사용하며 응용 용도가 단순하므로 높은 사양을 줄 필요가 없기 때문이다.
FIR filter designed with http://t-filter.appspot.com
sampling frequency: 4800 Hz
fixed point precision: 8 bits
* 0 Hz - 1000 Hz
gain = 1
desired ripple = 25 dB
* 1200 Hz - 2400 Hz
gain = 0
desired attenuation = -40 dB
아듀이노 보드는 아날로그-디지털 변환기 ADC(Analog-to-Digital Converter)를 내장한 8비트 마이크로 컨트롤러를 채택하고 있다. 동작 속도는 16Mhz로 꽤 빠르다. 실제로 소출력 단파 대역에 대응하는 소출력 아마추어 무선용 무전기의 중앙 처리기로 사용되고 있다[바로가기]. 위의 조건에 맞는 저대역 통과 FIR 필터의 계수는 아래와 같이 구해졌다.
uint8_t filter_taps[FILTER_TAP_NUM] = {
4, 12, 25, 34, 34, 25, 12, 4 };
이제 '급수합'의 식을 C 언어로 표현해 보자.
void fir ( acc_t *y, data_t x)
{
static data_t shift_reg[FILTER_TAP_NUM];
acc_t acc;
data_t data;
coef_t c;
int i;
acc=0;
for (i=FILTER_TAP_NUM-1;i>=0;i--)
{
if (i==0)
{
shift_reg[0]=x;
data = x;
}
else
{
shift_reg[i] = shift_reg[i-1];
data = shift_reg[i];
}
c = filter_taps[i];
acc += data*c;
}
*y=acc;
}
필터의 계수 만큼 곱셈과 덧셈을 반복하여 그 합을 구한다. 계산이 진행되는 흐름을 도식으로 표현하면 아래와 같다.

매우 단순해 보이는 이 프로그램이 낳을 마법을 알아보기 위해 시험을 해봤다. 위상을 각각 임의로 준 51Hz, 700Hz, 1.9Khz, 2.1Khz 의 정현파에 총 진폭의 20 퍼센트 가량의 백색 잡음을 섞어 입력 신호로 사용 했다.
x[t] = (AMPLITUDE/16*(cos((2*M_PI/F_SAMPLE) * 51.0 * t + (float)(rand()%10)/10.0)+1))
+ (AMPLITUDE/ 8*(cos((2*M_PI/F_SAMPLE) * 700.0 * t + (float)(rand()%30)/30.0)+1))
+ AMPLITUDE/ 4*(cos((2*M_PI/F_SAMPLE) * 1900.0 * t + (float)(rand()%50)/50.0)+1))
+ (AMPLITUDE/ 4*(cos((2*M_PI/F_SAMPLE) * 2100.0 * t + (float)(rand()%70)/70.0)+1))
+ (Xin[t]+NOISE_RANGE);
입력 신호의 모습은 아래와 같다.

잡음과 몇개의 유효신호가 합쳐져 시간의 축 상에서 보면 의미를 찾아보기 어렵다. 퓨리에 변환을 수행하여 주파수 축으로 보면 아래와 같다. 진폭이 AMPLITUDE/16에 불과한 51Hz의 신호는 거의 잡음속에 묻혀있다. 상대적으로 큰 신호인 700hz의 신호는 뚜렸하다. 그외 1.9Khz와 2.1Khz의 신호는 비교적 진폭이 컷음에도 두렸한 존재감을 보여주지 못하고 있다. 오히려 고조파 왜곡이 일어나고 있다.

필터를 거친 후 출력의 모습이다. 잡음이 상당히 억제되어 있다. 지속적인 '급수합'으로 인해 신호의 진폭 범위가 상당히 커졌다. 하지만 발산하지 않는다. 이는 신호처리 수식의 안정을 담보하며 계수를 구하기 때문이다.

어떤 주파수 성분이 살아남았는지 보기 위해 스펙트럼을 살펴보면 아래와 같다. 잡음속에 묻혀있던 50Hz의 신호가 확연히 드러난다. 차단 범위에 있던 신호들은 상당히 억제된 모습을 보여준다.

SSB 무전기의 음성신호에 전신 수신용으로 사용할 FIR 저역 통과 필터를 시험해 봤다. 디지털 신호처리의 강점을 단적으로 보여준다. 디지털 방식의 신호처리는 계산의 정밀도에 의해 영향을 받는다. 하지만 아날로그 L-C 필터의 눈물 겨움에 비하면 수고랄 것도 없다. 사정이 이러니 디지털 방식에 열광하지 않을 수 없다. 다만 '정통' 아마추어 무선사로써 아쉽다면 소위 찝찔한 송진내도, 따끔한 인두기의 손맛도, 백열등 불빛의 은근함은 없다. 오래된 무전기에서 지난날을 회상해 보는 것도 '정통' 아마추어 무선 취미가로써 한 재미일 터다. 그런 '재미'를 알리 없는 다음 세대에게 이 취미를 물려 주려면 그들의 방식도 이해해 보기로 한다.