[HAM] 위상변조의 개념을 그림으로 확인하니 개운한 기분이 든다.

[HAM] 위상변조의 개념을 그림으로 확인하니 개운한 기분이 든다.

일전에 '디지탈 데이터 변조/위상천이 키잉(PSK)'에 관한 글[링크]을 써놓고 내내 개운치가 않았다. 실험/실습이 곤란 하더라도 연습이 빠진 글은 아무래도 공학적이지 않으니까. 찝찝한 마음에 몇일 잠도 오지 않았다[미친거아냐?]  궁리 끝에 '위상천이 키잉(위상변조)'의 의미를 보여주는 간단한 예제를 작성하고 난 지금 조금 개운하다[역시 미친거야!]

------------------------------------------------

[실습] QPSK를 울프람 언어로 구현해서 그림으로 확인해 보자 (봐야 믿는 거니까!)

(* Carriers: f=100 *)

carrierI = Table[Sqrt[2]*Cos[100*t], {t, 0, 2*Pi, (2*Pi)/600}];

carrierQ = Table[Sqrt[2]*Sin[100*t], {t, 0, 2*Pi, (2*Pi)/600}];

(* Binary Baseband Data *)

bitStream = Table[{1,1,0,0,0,1,1,0}];

(* Phase Shift Keying *)

Do[

    (* Bit-Stream De-Muxing & Zero-Crossing(Analog Signals) *)

    symbolI = If[bitStream[[2*n-1]]==0, -1, 1] ;

    symbolQ = If[bitStream[[2*n]]==0, -1, 1];

    

    (* Symbol out: Multiply De-Mux'ed Bit-Stream with I/Q Carriers*)

    modulated[[n]] = symbolI*carrierI + symbolQ*carrierQ;

    

    (* See I/Q-Mapped 2-Bits Symbol *)

    fModulated[[n]] = Fourier[modulated[[n]]];

, {n, 4}

]

입력: 2진 디지털 데이터 (bitStream)

(* Input: Binary Baseband Data *)
ListPlot[bitStream, PlotStyle->PointSize[Large]]

출력: 부반송파 주파수 f=100 로 변조된 심볼(modulated)

(* PSKed Out Symbol in Time-Domain *)

ListLinePlot[
    {modulated[[1]],modulated[[2]],modulated[[3]],modulated[[4]]},
    PlotRange->{{0,40}, {-2, 2}},
    PlotLegends->{

        "Symbol[+1,+1]",

        "Symbol[+1,-1]",

        "Symbol[-1,-1]",

        "Symbol[-1,1]"}
]

시간영역(Time-Domain)에서 보면 4가지 심볼은 구분할 수 없다.

주파수영역(Frequency-Domain)으로 변환해 보자.

• 파워 스펙트럼(Power Spectrum)으로 보면 4가지 심볼 모두 동일하게 반송파 주파수 f=100 에서 최대 전력으로 나타난다. 즉, 주파수 및 진폭변화 없음

(* PSKed Symbol in Frequency-Domain *)
ListLinePlot[
    {
        Abs[fModulated[[1]]][[1;;300]],
        Abs[fModulated[[2]]][[1;;300]],
        Abs[fModulated[[3]]][[1;;300]],
        Abs[fModulated[[4]]][[1;;300]]
    }, PlotRange->All,
    PlotLegends->{

        "Symbol[+1,+1]",

        "Symbol[+1,-1]",

        "Symbol[-1,-1]",

        "Symbol[-1,1]"}

]

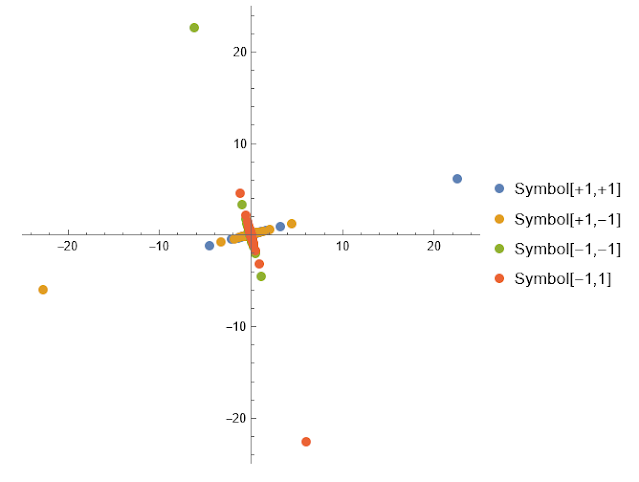
• 위상공간(I/Q-Phase Plane)에서는 최대 전력이 찍히는 성상점(Constellation)의 위치가 분명히 드러난다. 즉, 디지털 데이터의 위상변조다.

(* I/Q Plane (Phase Constellation) *)

ComplexListPlot[

    {

        fModulated[[1]][[1;;300]],

        fModulated[[2]][[1;;300]],

        fModulated[[3]][[1;;300]],

        fModulated[[4]][[1;;300]]

    }, PlotRange->{{-17,17}, {-17,17}},

    PlotStyle->PointSize[Large],

    PlotLegends->{

        "Symbol[+1,+1]",

        "Symbol[+1,-1]",

        "Symbol[-1,-1]",

        "Symbol[-1,1]"}

]

----------------------------------------------------------------